Chapter 9 - Conservation of chemical-species mass¶
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from scipy.linalg import expm
Trace elements¶
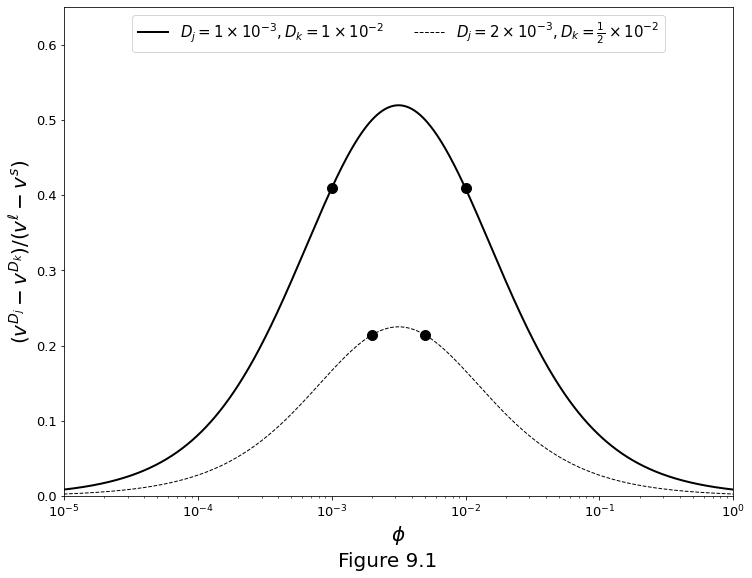
Segregation rate of two trace elements by equilibrium transport as a function of porosity, according to equation
\[
\begin{equation}
\label{eq:trace-segregation-rate}
\frac{v^{\dico_j} - v^{\dico_k}}{v\liq-v\sol} =
\frac{\por\liq(\dico_k-\dico_j)}{(\por\liq+\dico_j)(\por\liq+\dico_k)}.
\end{equation}
\]
The curve is plotted in Figure 9.1 for two sets of \(D_j,D_k\). Note the speed difference between the two trace elements is plotted as a fraction of the speed difference between liquid and solid.
fig, ax = plt.subplots()
fig.set_size_inches(12.0, 9.0)
Dj = 1e-3
Dk = 1e-2
phi = np.logspace(-5., 0., 1000)
f = phi*(Dk-Dj)/(phi+Dj)/(phi+Dk)
Djs = 2e-3
Dks = 0.5e-2
fs = phi*(Dks-Djs)/(phi+Djs)/(phi+Dks)
ax.semilogx(
phi, f, '-k', linewidth=2,
label=r'$D_j=1\times10^{-3},D_k=1\times10^{-2}$'
)
ax.plot([Dj, Dk], np.interp([Dj, Dk], phi, f), 'ok', markersize=10)
ax.semilogx(
phi, fs, '--k', linewidth=1,
label=r'$D_j=2\times10^{-3},D_k=\frac{1}{2}\times10^{-2}$'
)
ax.plot(
[Djs, Dks], np.interp([Djs, Dks], phi, fs),
'ok', markersize=10
)
ax.set_xlim(1e-5, 1e0)
ax.set_ylim(0.0, 0.65)
ax.set_xticks((1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1e0))
ax.set_yticks((0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6))
ax.set_xlabel(r'$\phi$', fontsize=20)
ax.set_ylabel(r'$(v^{D_j}-v^{D_k})/(v^\ell-v^s)$', fontsize=20)
ax.legend(loc='upper center', fontsize=15, ncol=2)
ax.tick_params(axis='both', which='major', labelsize=13)
fig.supxlabel("Figure 9.1", fontsize=20)
plt.show()
Closed-system evolution of a decay chain¶
Evolution with melting only¶
The batch melting equation, parametrised as a function of time, is given by
\[
\begin{equation}
\label{eq:closedbox-batch-soln}
\con\liq_j(t) = \frac{\con\sol_j\vert_0}
{\dico_j + (1-\dico_j)\boxmeltrate t}.
\end{equation}
\]
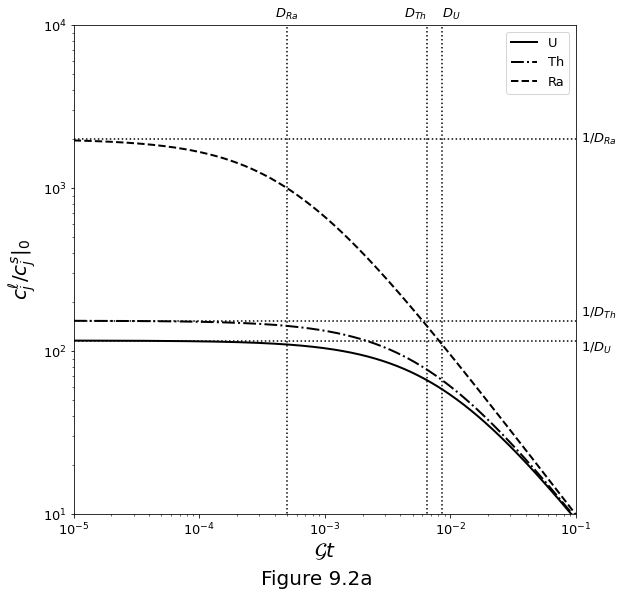
Figure 9.2 below plots the closed system evolution of the uranium-series decay chain under melting only.
fig, ax = plt.subplots()
fig.set_size_inches(9.0, 9.0)
lamb_ = np.asarray([1.5e-10, 9.19e-6, 4.33e-4])
D = np.asarray([0.0086, 0.0065, 0.0005])
lsty = ['-', '-.', '--']
labl = [r'$D_{U}$', r'$D_{Th}$', r'$D_{Ra}$']
labm = [r'$1/D_{U}$', r'$1/D_{Th}$', r'$1/D_{Ra}$']
alh = ['left', 'right', 'center']
alv = ['top', 'bottom', 'center']
Gt = np.logspace(-5.0, -1.0, 1000)
clocs = np.asarray([np.power(di + (1.-di)*Gt, -1.0) for di in D])
lines = []
for clocsi, lstyi, Di, labli, alhi, labmi, alvi in zip(
clocs, lsty, D, labl, alh, labm, alv
):
lines.append(
plt.loglog(
Gt, clocsi,'k', linewidth=2, linestyle=lstyi
)[0]
)
ax.plot([Di, Di], [1e-10, 1e10], ':k')[0]
ax.plot([1e-5, 1e-1], [1./Di, 1./Di], ':k')[0]
ax.text(
Di, 10.1**4, labli, fontsize=13,
verticalalignment='bottom', horizontalalignment=alhi
)
ax.text(
0.11, 1./Di, labmi, fontsize=13,
horizontalalignment='left', verticalalignment=alvi
)
ax.set_xlim(1e-5, 1e-1)
ax.set_ylim(1e1, 1e4)
ax.set_xticks((1e-5, 1e-4, 1e-3, 1e-2, 1e-1))
ax.set_yticks((1e1, 1e2, 1e3, 1e4))
ax.set_xlabel(r'$\mathcal{G}t$', fontsize=20)
ax.set_ylabel(r'$c^\ell_j/c^s_j\vert_0$', fontsize=20)
ax.legend(
handles=lines, labels=['U', 'Th', 'Ra'],
loc='upper right', fontsize=13
)
ax.tick_params(axis='both', which='major', labelsize=13)
fig.supxlabel("Figure 9.2a", fontsize=20)
plt.show()
Evolution due to ingrowth only¶
The decay chain of N elements under the ingrowth assumption is given by
\[
\begin{equation}
\label{eq:closedbox-solution-nomelting}
\actvec\liq(t) = \eigenvecs ~ \e^{\ddecaymatrix t} ~ \eigenvecs^{-1} ~ \actvec\liq\vert_0.
\end{equation}
\]
Figure 9.2b below plots the closed system evolution of the uranium-series decay chain under ingrowth only.
def eigenvectors(lamb_):
l_ = len(lamb_)
V = np.zeros(l_*l_, dtype=np.float128).reshape(l_, l_)
iV = np.zeros(l_*l_, dtype=np.float128).reshape(l_, l_)
for i in np.arange(0, l_):
for j in np.arange(0, i+1):
tmp = 1.
for m in np.arange(i+1, l_):
tmp = tmp*(lamb_[m]-lamb_[j])/lamb_[m]
V[i, j] = tmp
for i in np.arange(0, l_):
for j in np.arange(0, i+1):
tmp = 1.
for m in np.arange(j, l_):
if m != i:
tmp = tmp/(lamb_[m]-lamb_[i])
for m in np.arange(j+1, l_):
tmp = tmp*lamb_[m]
iV[i, j] = tmp
return V, iV
fig, ax = plt.subplots()
fig.set_size_inches(9.0, 9.0)
lambda_ = np.asarray(
[1.5e-10, 2.83e-6, 9.19e-6, 4.33e-4],
dtype=np.float128
)
D = np.asarray(
[0.0086, 0.0086, 0.0065, 0.0005],
dtype=np.float128
)
lsty = ['-',':','-.','--']
labl = [
r'$\tau_{1/2}^{(238U)}$', r'$\tau_{1/2}^{(234U)}$',
r'$\tau_{1/2}^{(230Th)}$', r'$\tau_{1/2}^{(226Ra)}$'
]
alv = ['bottom','bottom','bottom','bottom']
tmax = 11.0
t = np.logspace(0.0, tmax, 1000, dtype=np.float128)
al0 = np.asarray([1.0, 5.0, 2.0, 1.0], dtype=np.float128)/D
Ld = np.diag(-lambda_).astype(np.float128)
V, Vi = eigenvectors(lambda_)
expmLd = np.asarray([np.diag(expm(Ld*tj)) for tj in t])
expmLd = np.asarray([np.diag(eLd) for eLd in expmLd])
al = np.asarray(
[np.dot(np.dot(np.dot(V, eLd), Vi), al0) for eLd in expmLd]
)
lines = []
for ali, lstyi, lambdai, labli, alvi in zip(al.transpose(), lsty, lambda_, labl, alv):
lines.append(
plt.loglog(
t, ali, 'k', linewidth=2, linestyle=lstyi
)[0]
)
ax.plot(
[np.log(2.)/lambdai, np.log(2.)/lambdai], [1e-10, 1e10],
':k'
)
ax.text(
np.log(2.)/lambdai, 1e4, labli, fontsize=15,
rotation=60, verticalalignment=alvi, horizontalalignment='left'
)
ax.set_xlim(1e1, 10**tmax)
ax.set_ylim(1e1, 1e4)
ax.set_xticks((1e2, 1e4, 1e6, 1e8, 1e10))
ax.set_yticks((1e1, 1e2, 1e3, 1e4))
ax.set_xlabel(r'$t$, yr', fontsize=20)
ax.set_ylabel(r'$a^\ell_j$, yr$^{-1}$', fontsize=20)
ax.tick_params(axis='both', which='major', labelsize=13)
ax.legend(
handles=lines, loc='upper right', fontsize=15,
labels=['$^{238}$U', '$^{234}$U', '$^{230}$Th', '$^{226}$Ra'],
)
fig.supxlabel("Figure 9.2b", fontsize=20)
plt.show()
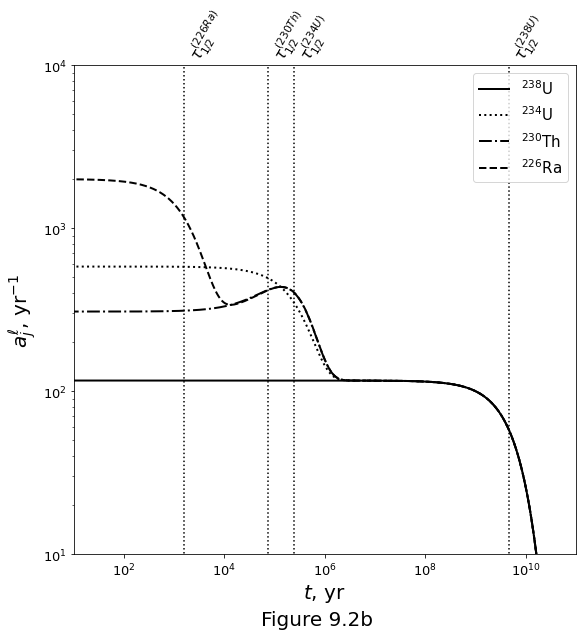
Evolution by both melting and ingrowth¶
The decay chain of N elements when melting and ingrowth processes are occurring simultaneously is given by
\[
\begin{equation}
\label{eq:closedbox-solution}
\actvec\liq(t) = \eigenvecs ~ \e^{\ddecaymatrix t} ~ \eigenvecs^{-1} ~
\left[ \frac{\actvec\sol\vert_0}{\dicovec + (1-\dicovec)\boxmeltrate t} \right]
\end{equation}
\]
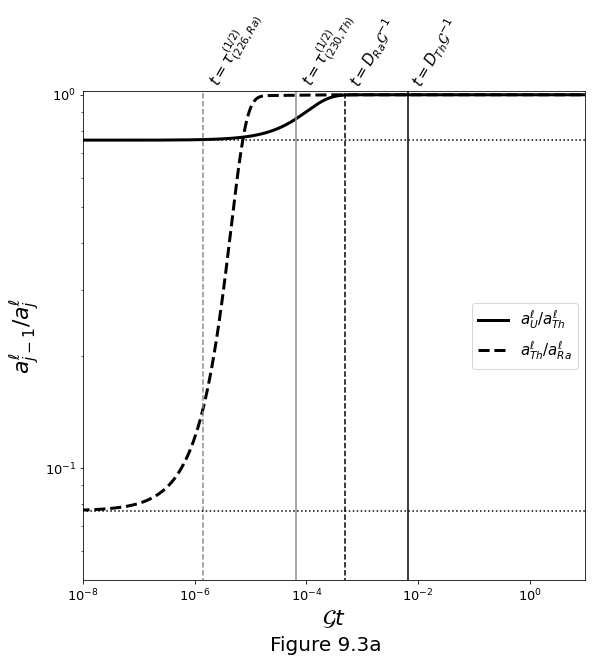
The activities are plotted below in terms of parent/daughter isotope ratios as a function of \(\mathcal{G} t\), which corresponds to \(F\) for values up to unity (at which \(F\) is capped). Vertical lines mark key time-scales for ingrowth and melting. Horizontal lines mark the \(D\) ratios of parent–daughter pairs that control the initial elemental fractionation (for small \(F\)).
Slow melting: \(\mathcal{G}=\frac{1}{100} D_\textrm{Th} \big/ \tau^{(1/2)}_\textrm{Th}\)¶
Figure 9.3a below plots evolution for a slow melting rate, in which activity ratios go to secular equilibrium by ingrowth.
fig, ax = plt.subplots()
fig.set_size_inches(9.0, 9.0)
Dtag = [
'', r'D_{U}', r'D_{Th}', r'D_{Ra}'
]
Ttag = [
'', '', r'\tau^{(1/2)}_{(230,Th)}', r'\tau^{(1/2)}_{(226,Ra)}'
]
Ttag_height = np.asarray(
[0.6, 0.6, 0.6], dtype=np.float128
)
lambda_ = np.asarray(
[1.5e-10, 2.83e-6, 9.19e-6, 4.33e-4], dtype=np.float128
)
D = np.asarray(
[0.0086, 0.0086, 0.0065, 0.0005], dtype=np.float128
)
Q = lambda_[2:]*D[2:]/np.log(2.)
G = np.amin(Q)/100.
as0 = np.asarray([1., 1., 1., 1.], dtype=np.float128)
lsty = ['-','--']
as0 = np.asarray([1., 1., 1., 1.])
grey = 0.55
t = np.logspace(-10., 11., 1000, dtype=np.float128) * G
Ld = np.diag(-lambda_/G).astype(np.float128)
V, Vi = eigenvectors(lambda_)
F = np.minimum(t, 1., dtype=np.float128)
expmLd = np.asarray([np.diag(expm(Ld*tj)) for tj in t])
expmLd = np.asarray([np.diag(eLd) for eLd in expmLd])
VeLdVi = np.asarray([np.dot(V, np.dot(eLd, Vi)) for eLd in expmLd])
ald = np.asarray([np.dot(VeVi, as0/D) for VeVi in VeLdVi])
al = np.asarray(
[np.dot(VeVi, as0/(D + (1.-D)*f)) for VeVi, f in zip(VeLdVi, F)]
)
alb = np.asarray([as0/(D + (1-D)*f) for f in F])
lines = []
for i in np.arange(2, len(lambda_)):
lines.append(
plt.loglog(t, al[:, i-1]/al[:, i], 'k',
linewidth=3, linestyle=lsty[i-2])[0]
)
ax.plot(
[np.log(2.)/(lambda_[i]/G), np.log(2)/(lambda_[i]/G)],
[1e-10, 1e10], linestyle=lsty[i-2], color=[grey, grey, grey]
)
ax.plot([D[i], D[i]], [1e-10, 1e10], 'k', linestyle=lsty[i-2])
ax.plot([1e-10, 1e3], [D[i]/D[i-1], D[i]/D[i-1]], ':k')
ax.text(
np.log(2.)/(lambda_[i]/G), 1.025, f'$t={Ttag[i]}$',
fontsize=15, rotation=60,
verticalalignment='bottom', horizontalalignment='left'
)
ax.text(
D[i], 1.025, f'$t={Dtag[i]}'+'\mathcal{G}^{-1}$',
fontsize=15, rotation=60,
verticalalignment='bottom', horizontalalignment='left'
)
ax.set_xlim(1e-8, 1e1)
ax.set_ylim(np.power(10., -1.3), np.power(10., 0.01))
ax.set_xticks((1e-8, 1e-6, 1e-4, 1e-2, 1e0))
ax.set_yticks((1e-1, 1e0))
ax.set_ylabel(r'$a^\ell_{j-1}/a^\ell_j$', fontsize=22)
ax.set_xlabel(r'$\mathcal{G}t$', fontsize=22)
ax.tick_params(axis='both', which='major', labelsize=13)
ax.legend(
handles=lines, loc='center right', fontsize=15,
labels=[r'$a^\ell_{U} /a^\ell_{Th}$', r'$a^\ell_{Th}/a^\ell_{Ra}$']
)
fig.supxlabel("Figure 9.3a", fontsize=20)
plt.show()
Fast melting: \(\mathcal{G}=100 D_\textrm{Ra} \big/ \tau_\textrm{Ra}^{(1/2)}\)¶
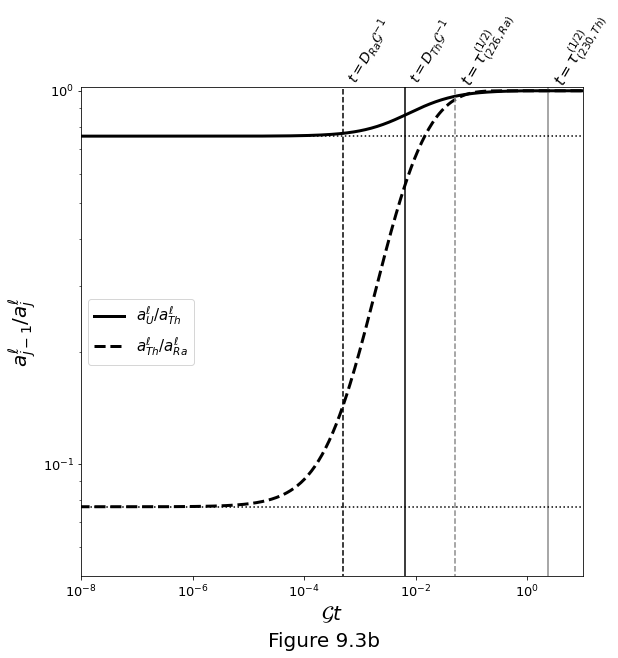
Figure 9.3b below plots evolution for a fast melting rate. Activity ratios go to secular equilibrium by dilution back to the activities of the solid (which were in secular equilibrium initially).
fig, ax = plt.subplots()
fig.set_size_inches(9.0, 9.0)
Dtag = [
'', r'D_{U}', r'D_{Th}', r'D_{Ra}'
]
Ttag = [
'', '', r'\tau^{(1/2)}_{(230,Th)}', r'\tau^{(1/2)}_{(226,Ra)}'
]
Ttag_height = np.asarray(
[0.6, 0.6, 0.6], dtype=np.float128
)
lambda_ = np.asarray(
[1.5e-10, 2.83e-6, 9.19e-6, 4.33e-4],
dtype=np.float128
)
D = np.asarray(
[0.0086, 0.0086, 0.0065, 0.0005],
dtype=np.float128
)
Q = lambda_[2:]*D[2:]/np.log(2.)
G = np.amax(Q)*100.
as0 = np.asarray([1., 1., 1., 1.], dtype=np.float128)
lsty = ['-','--']
as0 = np.asarray([1., 1., 1., 1.])
grey = 0.55
t = np.logspace(-10., 11., 1000, dtype=np.float128) * G
Ld = np.diag(-lambda_/G).astype(np.float128)
V, Vi = eigenvectors(lambda_)
F = np.minimum(t, 1., dtype=np.float128)
expmLd = np.asarray([np.diag(expm(Ld*tj)) for tj in t])
expmLd = np.asarray([np.diag(eLd) for eLd in expmLd])
VeLdVi = np.asarray(
[np.dot(V, np.dot(eLd, Vi)) for eLd in expmLd]
)
ald = np.asarray([np.dot(VeVi, as0/D) for VeVi in VeLdVi])
al = np.asarray(
[np.dot(VeVi, as0/(D + (1.-D)*f)) for VeVi, f in zip(VeLdVi, F)]
)
alb = np.asarray([as0/(D + (1-D)*f) for f in F])
lines = []
for i in np.arange(2, len(lambda_)):
lines.append(
plt.loglog(
t, al[:, i-1]/al[:, i], 'k',
linewidth=3, linestyle=lsty[i-2]
)[0]
)
ax.plot(
[np.log(2.)/(lambda_[i]/G), np.log(2)/(lambda_[i]/G)],
[1e-10, 1e10], linestyle=lsty[i-2],
color=[grey, grey, grey]
)
ax.plot([D[i], D[i]], [1e-10, 1e10], 'k', linestyle=lsty[i-2])
ax.plot([1e-10, 1e3], [D[i]/D[i-1], D[i]/D[i-1]], ':k')
ax.text(
np.log(2.)/(lambda_[i]/G), 1.0, f'$t={Ttag[i]}$',
fontsize=15, rotation=60,
verticalalignment='bottom', horizontalalignment='left'
)
ax.text(
D[i], 1.025, f'$t={Dtag[i]}'+'\mathcal{G}^{-1}$',
fontsize=14, rotation=60,
verticalalignment='bottom', horizontalalignment='left'
)
ax.set_xlim(1e-8, 1e1)
ax.set_ylim(np.power(10., -1.3), np.power(10., 0.01))
ax.set_xticks((1e-8, 1e-6, 1e-4, 1e-2, 1e0))
ax.set_yticks((1e-1, 1e0))
ax.set_ylabel(r'$a^\ell_{j-1}/a^\ell_j$', fontsize=20)
ax.set_xlabel(r'$\mathcal{G}t$', fontsize=20)
ax.legend(
handles=lines, loc='center left', fontsize=15,
labels=[r'$a^\ell_{U} /a^\ell_{Th}$', r'$a^\ell_{Th}/a^\ell_{Ra}$']
)
ax.tick_params(axis='both', which='major', labelsize=13)
fig.supxlabel("Figure 9.3b", fontsize=20)
plt.show()
