Chapter 14 - Numerical modelling of two-phase flow¶
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import brentq
import scipy.sparse as sp
import scipy.sparse.linalg as spla
import warnings
warnings.filterwarnings('ignore')
The 1-D solitary wave (instantaneous)¶
The compaction equation reads
\[
\begin{equation}
\label{eq:num-cmp-eqn}
\diff{}{z}\npor^\permexp\diff{\cmp}{z} - \cmp = \diff{\npor^\permexp}{z}.
\end{equation}
\]
Finite Difference Discretisation¶
The finite-difference form of equation \(\eqref{eq:num-cmp-eqn}\) is
\[
\begin{equation}
\label{eq:num-cmpeqn-stencil}
\left[\begin{array}{ccc}
\npor^\permexp_{i-1/2}, & -\left(\Dz^2+\npor^\permexp_{i-1/2}+
\npor^\permexp_{i+1/2}\right), & \npor^\permexp_{i+1/2}
\end{array} \right]\aprx{\cmp}_i = \Dz\left(\npor_{i+1/2}^\permexp -
\npor_{i-1/2}^\permexp\right).
\end{equation}
\]
NOTE: In stencil notation, multiplication of a stencil \(\left[S_a,\;\;S_b,\;\;S_c\right]\) with a discrete variable \(q_i\) is computed as \(S_aq_{i-1} + S_bq_{i} + S_cq_{i+1}\)}.
To make progress toward solving for \(\aprx{\cmp}_i\), we write \(\eqref{eq:num-cmpeqn-stencil}\) in the form \(\mathbf{A}\posvec = \boldsymbol{b}\), where \(\boldsymbol{b}\) is a column vector with \(b_i=\Dz\left(\npor_{i+1/2}^\permexp - \npor_{i-1/2}^\permexp\right)\). The unknowns go into column vector \(\posvec\). The stencil is used to fill a tridiagonal band in the matrix \(\mathbf{A}\). The first and last rows in \(\mathbf{A}\) and \(\boldsymbol{b}\) are constructed to satisfy the boundary conditions. The result is
\[\begin{split}
\begin{equation}
\label{eq:num-fd-matrix-equation}
\left(\begin{array}{cccccc}
1 & 0 & & & & \\[1mm]
[\,\, & S_2 & \,\,] & & & \\[1mm]
& [\,\, & S_3 & \,\,] & & \\[1mm]
& & & \ddots & & \\[1mm]
& & & [\,\, & S_{N_z-1}& \,\,] \\[1mm]
& & & & 0 & 1 \end{array}\right)
\left(\begin{array}{c}\aprx{\cmp}_1 \\[1mm] \aprx{\cmp}_2 \\[1mm]
\aprx{\cmp}_3 \\[1mm] \vdots \\[1mm] \aprx{\cmp}_{N_z-1} \\[1mm]
\aprx{\cmp}_{N_z}\end{array}\right) =
\left(\begin{array}{c} 0 \\[1mm]
b_2 \\[1mm] b_3 \\[1mm] \vdots \\[1mm]
b_{N_z-1} \\[1mm] 0\end{array}\right),
\end{equation}
\end{split}\]
where \([\;\;S_i\;\;]\) is the \(i^\text{th}\) stencil, given in equation \(\eqref{eq:num-cmpeqn-stencil}\) above.
The Python function below solves the system \(\mathbf{A}\posvec = \boldsymbol{b}\):
def SolveCompactionRateFiniteDifference(phi, dz):
# matrix size
n_ = len(phi)
# form permeability
K = np.power(0.5*(phi[0:-1] + phi[1:]), par.n)
# form RHS
b = np.zeros(n_, dtype=float)
b[1:-1] = dz*(K[1:] - K[0:-1])
# create sparse matrix
offsets = np.array([0, -1, 1])
data = np.zeros(3 * n_).reshape(3, n_)
data[0, 0] = data[0, -1] = 1
data[0, 1:-1] = -(dz*dz + K[0:-1] + K[1:]) # diagonal
data[1, 0:-2] = K[0:-1] # sub-diagonal
data[2, 2:] = K[1:] # sup-diagonal
mtx = sp.dia_matrix((data, offsets), shape=(n_, n_))
mtx = mtx.tocsr()
x = spla.dsolve.spsolve(mtx, b)
return x
Finite Element Discretisation¶
The Finite Element form of equation \eqref{eq:num-cmp-eqn} is
\[
\begin{equation}
\label{eq:num-solwave-discrete-elementwise}
\sum_{i=1}^{N_z}c_i\int_{\Omega_e} \left(K\basis_e^\prime\basis_i^\prime +
\basis_e\basis_i\right)\infd\Omega =
\int_{\Omega_e} K\basis_e^\prime\infd\Omega.
\end{equation}
\]
Equation \(\eqref{eq:num-solwave-discrete-elementwise}\) can be expressed in terms of a matrix-vector product \(\mathbf{A}\boldsymbol{x} = \boldsymbol{b}\), where
\[\begin{split}
\begin{align*}
\mathbf{A} &= \sum_e \int_{\Omega_e} \left(K\basis_e^\prime\basis_i^\prime +
\basis_e\basis_i\right)\infd\Omega \\
\boldsymbol{b} &= \sum_e \int_{\Omega_e} K\basis_e^\prime\infd\Omega,
\end{align*}
\end{split}\]
and the vector of unknowns \(\boldsymbol{x}\) represents the coefficients \(c_i\). In the equation above, \(\sum_e\) is the assembly operator. To clarify the assembly operation, we write the bilinear and linear forms evaluated over one element \(\Omega_j\), which is written as the sub-matrix and sub-vector
\[\begin{split}
\begin{align}
\mathbf{A}^{\Omega_e} &= \int_{\Omega_e}
\left(\begin{array}{cc}
K\basis_j^\prime\basis_j^\prime + \basis_j\basis_j
& K\basis_j^\prime\basis_{j+1}^\prime + \basis_j\basis_{j+1} \\
K\basis_{j+1}^\prime\basis_j^\prime + \basis_{j+1}\basis_j
& K\basis_{j+1}^\prime\basis_{j+1}^\prime + \basis_{j+1}\basis_{j+1}
\end{array}\right)\infd\Omega,\\
\label{eq:num-solwave-linear-form-subvec}
\boldsymbol{b}^{\Omega_e} &= \int_{\Omega_e} \left(\begin{array}{c}
K\basis_{j}^\prime \\
K\basis_{j+1}^\prime
\end{array}\right)\infd\Omega.
\end{align}
\end{split}\]
Then the assembly of the global matrix \(\mathbf{A}\) and global vector \(\boldsymbol{b}\) involve summing the entries of \(\mathbf{A}^{\Omega_e}\) and \(\boldsymbol{b}^{\Omega_e}\) into the correct locations (recalling that \(\mathbf{A}\) is symmetrical).
The Python function below solves the system \(\mathbf{A}\boldsymbol{x} = \boldsymbol{b}\):
def SolveCompactionRateFiniteElement(phi, dz):
# number of nodes
N = len(phi)
# number of elements
N_elements = N - 1
# allocate memory
A = sp.dok_matrix((N, N), dtype=np.double)
# allocate memory
b = np.zeros(N, dtype=np.double)
# loop over elements
for e in range(N_elements):
A[e:e+2, e:e+2] = 0. # initializing matrix
Me = sp.dok_matrix([[1./dz, -1./dz], [-1.0/dz, 1./dz]], dtype=np.double)
Ce = sp.dok_matrix([[dz/3., dz/6.], [dz/6., dz/3.]], dtype=np.double)
re = np.asarray([-1.0, 1.0], dtype=np.double)
# form permeability at element centres
K = np.power(0.5 * (phi[0:-1] + phi[1:]), par.n)
# loop over elements
for e in range(N_elements):
# element bilinear form
Ae = Me * K[e] + Ce
be = re * K[e] # element linear form
A[e:e+2, e:e+2] += Ae # assemble global matrix
b[e:e+2] += be # assemble global RHS
A[[0, -1], [0, -1]] = 1.0
A[[0, -1], [1, -2]] = 0.0 # zero boundary rows
b[0] = b[-1] = 0 # boundary condition
A = A.tocsr()
# solve
x = spla.dsolve.spsolve(A, b)
return x
The analytical solution of the compact equation \(\eqref{eq:num-cmp-eqn}\) is given by
def xi(f, A):
return -np.sqrt(A + 0.5) * (
-2. * np.sqrt(A - f) + np.log(
(
np.sqrt(A - 1.)-np.sqrt(A - f)
) / (
np.sqrt(A - 1.)+np.sqrt(A - f)
)
) / np.sqrt(A - 1.)
)
def SolitaryWaveGenerator(Amplitude, z, z0):
f = np.ones(z.shape[0])
zeta = np.abs(z-z0)
fEpsilon = 1.000000001
zetaEpsilon = xi(fEpsilon, Amplitude)
ifill = np.nonzero(zeta <= zetaEpsilon)
for i in ifill[0]:
f[i] = brentq(
lambda phi_: xi(phi_, Amplitude)-zeta[i],
fEpsilon,
Amplitude
)
return f
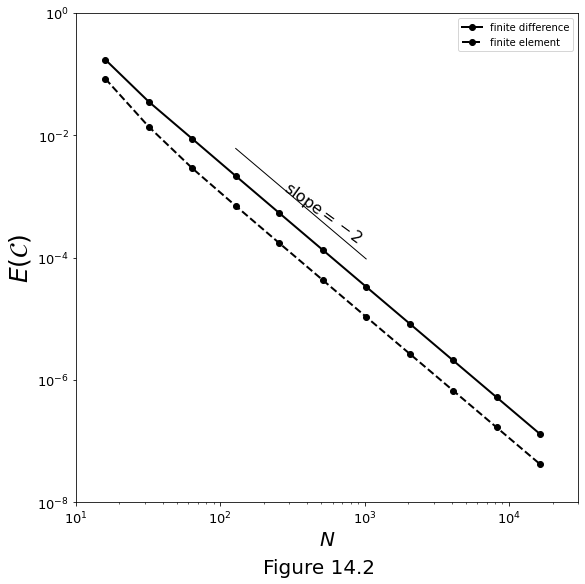
Figure 14.2 below plots the error \(\error\) versus number of nodes \(N_z\) for numerical solutions of the Compaction Equation \(\eqref{eq:num-cmp-eqn}\). The solid line marks the error for the finite difference method \(\eqref{eq:num-cmpeqn-stencil}\). The dashed line marks the error for the finite element method. The analytical solution is shown in chapter 6.
class PAR:
def __init__(
self, n=3, ls=4, zm=40,
ni=np.power(
2., [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
)
):
self.n = n
self.Ls = ls
self.V = 2*self.Ls + 1
self.zm = zm
self.ni = ni
par = PAR()
err_fd = np.zeros(len(par.ni))
err_fe = np.zeros(len(par.ni))
for n, ni in enumerate(par.ni):
z = np.linspace(-par.zm, par.zm, int(ni))
# semi-analytical solitary wave profile
phi = SolitaryWaveGenerator(par.Ls, z, 0)
# analytical compaction rate
a_cmp = np.sign(z) * np.sqrt(
-2. * par.V * (phi-1)**2 / phi**2 * (phi - (par.V-1.)/2.)
)
# numerical compaction rate
n_cmp_fd = SolveCompactionRateFiniteDifference(phi, z[1]-z[0])
n_cmp_fe = SolveCompactionRateFiniteElement(phi, z[1]-z[0])
# error
err_fd[n] = np.linalg.norm(a_cmp-n_cmp_fd, 2) / np.linalg.norm(a_cmp, 2)
err_fe[n] = np.linalg.norm(a_cmp-n_cmp_fe, 2) / np.linalg.norm(a_cmp, 2)
fig, ax = plt.subplots()
fig.set_size_inches(9., 9.)
# plotting
p1, = plt.loglog(par.ni, err_fd, '-ok', linewidth=2)
p2, = plt.loglog(par.ni, err_fe, '--ok', linewidth=2)
plt.loglog(
par.ni[3:7], 100*np.power(par.ni[3:7], -2), '-k', linewidth=1
)
plt.xlabel(r'$N$', fontsize=20)
plt.ylabel(r'$E(\mathcal{C})$', fontsize=25)
plt.text(
par.ni[5], 190*np.power(par.ni[6], -2), r'slope$=-2$',
fontsize=16, rotation=-36, horizontalalignment='center'
)
plt.xlim(10.0, 3.e4)
plt.ylim(1.e-8, 1.0)
plt.tick_params(axis='both', which='major', labelsize=13)
leg = plt.legend(
handles=[p1, p2], labels=['finite difference', 'finite element']
)
fig.supxlabel("Figure 14.2", fontsize=20)
plt.show()
A 2-D manufactured solution (instantaneous)¶
We seek numerical solutions to the instantaneous flow problem for a given, two-dimensional porosity field
\[\begin{split}
\begin{align}
\label{eq:num_mfcsol_gov_compaction}
-\Div\vel\sol + \Div\left[\mobility \left(\Grad\pres + \yhat\right)\right] &= \cmpforce, \\
\label{eq:num_mfcsol_gov_stokes}
-\Grad\pres + \delta^2\delsq\vel\sol + 2\delta^2\Grad\left(\Div\vel\sol\right)
- \por\yhat &= \stokesforce.
\end{align}
\end{split}\]
where all symbols are now dimensionless; \(\mobility = \left(\por/\por_0\right)^\permexp\) is the mobility, \(\yhat = \gravity/g\) is the direction of gravitational acceleration, and \(\delta = \cmplength_0/H\) is a non-dimensional compaction length (\(\cmplength_0\) is the reference, dimensional compaction length). \(\cmpforce\) and \(\stokesforce\) are obtained by substituting analytical functions \(\vel\sol_\manufac\) and \(\pres_\manufac\) (the manufactured solution) into the augmented governing equations \(\eqref{eq:num_mfcsol_gov_compaction}\)-\(\eqref{eq:num_mfcsol_gov_stokes}\).
A reasonable choice (among many) is
\[\begin{split}
\begin{align}
\label{eq:num-manufac-solution1}
\phi_\manufac &= \phi_0\left[1 + \phi^*\cos\left(m\pi x\right)\cos\left(m\pi y\right)\right],\\
\label{eq:num-manufac-solution2}
\pres_\manufac &= P^*\cos\left(m\pi x\right)\cos\left(m\pi y\right),\\
\label{eq:num-manufac-solution3}
\psi_\manufac &= -\psi^*\left[1 - \cos\left(m\pi x\right)\right]\left[1 - \cos\left(m\pi y\right)\right],\\
\label{eq:num-manufac-solution4}
\scalarpotential_\manufac &= \scalarpotential^* \cos\left(m\pi x\right)\cos\left(m\pi y\right),
\end{align}
\end{split}\]
These functions are implemented in Python below:
def MnfcSoln_phi(X, Y, par):
return par.phi0 * (
1.0
+ par.A_phi * np.cos(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
)
def MnfcSoln_psi(X, Y, par):
return par.A_psi * (
1.0 - np.cos(np.pi * par.m * X)
) * (
1.0 - np.cos(np.pi * par.m * Y)
)
def MnfcSoln_U(X, Y, par):
return par.A_U * \
np.sin(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
def MnfcSoln_P(X, Y, par):
return par.A_ * \
np.sin(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
def MnfcSoln_CurlPsi(X, Y, par):
Cpsi_x = par.A_psi * (
1.0 - np.cos(np.pi * par.m * X)
) * (
np.pi * par.m * np.sin(np.pi * par.m * Y)
)
Cpsi_y = -par.A_psi * (
np.pi * par.m * np.sin(np.pi * par.m * X)
) * (
1.0 - np.cos(np.pi * par.m * Y)
)
return Cpsi_x, Cpsi_y
def MnfcSoln_GradU(X, Y, par):
GU_x = par.A_U * \
np.pi * par.m * np.cos(np.pi * par.m * X) * \
np.sin(np.pi * par.m * Y)
GU_y = par.A_U * \
np.pi * par.m * np.sin(np.pi * par.m * X) * \
np.cos(np.pi * par.m * Y)
return GU_x, GU_y
def MnfcSoln_DelsqU(X, Y, par):
return -2.0 * np.pi**2 * par.m**2 * MnfcSoln_U(X, Y, par)
def MnfcSoln_GradDelsqU(X, Y, par):
GdelsqU_x, GdelsqU_y = MnfcSoln_GradU(X, Y, par)
GdelsqU_x = -2.0*np.pi**2 * par.m**2 * GdelsqU_x
GdelsqU_y = -2.0*np.pi**2 * par.m**2 * GdelsqU_y
return GdelsqU_x, GdelsqU_y
def MnfcSoln_GradP(X, Y, par):
GP_x = par.A_P * np.pi * par.m * \
np.cos(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
GP_y = par.A_P * np.pi * par.m * \
np.sin(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
return GP_x, GP_y
def MnfcSoln_VelS(X, Y, par):
Vx, Vy = MnfcSoln_CurlPsi(X, Y, par)
Vxc, Vyc = MnfcSoln_GradU(X, Y, par)
return Vx + Vxc, Vy + Vyc
class PAR:
def __init__(
self, m=2, n=3, phi0=0.01, delta=1,
a_psi=1.0, a_u=1.0, a_p=1.0, a_phi=0.1
):
self.m = m
self.n = n
self.phi0 = phi0
self.delta = delta
# amplitudes
self.A_psi = a_psi
self.A_U = a_u
self.A_P = a_p
self.A_phi = a_phi
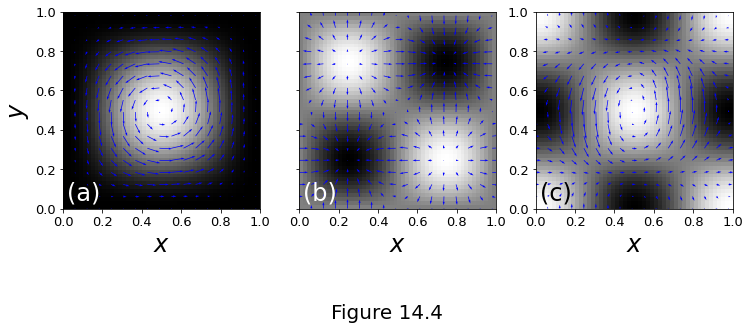
Figure 14.4 below plots the manufactured solution, computed using equations \(\eqref{eq:num-manufac-solution1}\)-\(\eqref{eq:num-manufac-solution4}\), for \(m=2\), \(\psi^*=\scalarpotential^*=1\), and \(\phi^*=0.1\). All quantities are dimensionless. The pressure \(\pres_\manufac\) is not shown. (a) The shear potential \(\psi_\manufac\) is shown in grayscale; vectors illustrate \(\Curl\psi_\manufac\zhat\), the incompressible part of the flow. (b) The compaction potential \(\scalarpotential_\manufac\) is shown in grayscale; vectors illustrate \(\Grad\scalarpotential_\manufac\), the compaction part of the flow. (c) The porosity \(\phi_\manufac\) is shown in grayscale; vectors illustrate the total solid flow field \(\vel\sol_\manufac\).
fig, ax = plt.subplots(1, 3)
fig.set_size_inches(12., 6.)
par = PAR()
N = 50
x = np.linspace(0, 1, N)
y = np.linspace(0, 1, N)
X, Y = np.meshgrid(x, y)
ss = 3
psi = MnfcSoln_psi(X, Y, par) # shear potential
ax[0].imshow(psi, cmap=plt.cm.gray, extent=[0, 1, 0, 1])
Vx, Vy = MnfcSoln_CurlPsi(X, Y, par)
ax[0].quiver(
X[0::ss, 0::ss], Y[0::ss, 0::ss],
Vx[0::ss, 0::ss], Vy[0::ss, 0::ss], color='b'
)
ax[0].set_xlabel('$x$', fontsize=24)
ax[0].set_xticklabels(
(0.0, 0.2, 0.4, 0.6, 0.8, 1.0), fontsize=20
)
ax[0].set_ylabel('$y$', fontsize=24)
ax[0].set_yticklabels(
(0.0, 0.2, 0.4, 0.6, 0.8, 1.0), fontsize=20
)
ax[0].text(
0.02, 0.02, r'(a)', fontsize=24,
verticalalignment='bottom', horizontalalignment='left',
color='white'
)
ax[0].tick_params(axis='both', which='major', labelsize=13)
U = MnfcSoln_U(X, Y, par)
Vx, Vy = MnfcSoln_GradU(X, Y, par)
ax[1].imshow(U, cmap=plt.cm.gray, extent=[0, 1, 0, 1])
ax[1].quiver(
X[0::ss, 0::ss], Y[0::ss, 0::ss],
Vx[0::ss, 0::ss], Vy[0::ss, 0::ss], color='b'
)
ax[1].set_xlabel('$x$', fontsize=24)
ax[1].set_xticklabels(
(0.0, 0.2, 0.4, 0.6, 0.8, 1.0), fontsize=20
)
ax[1].set_yticklabels(())
ax[1].text(
0.02, 0.02, r'(b)', fontsize=24,
verticalalignment='bottom', horizontalalignment='left',
color='white'
)
ax[1].tick_params(axis='both', which='major', labelsize=13)
phi = MnfcSoln_phi(X, Y, par)
Vx, Vy = MnfcSoln_VelS(X, Y, par)
ax[2].imshow(phi, cmap=plt.cm.gray, extent=[0, 1, 0, 1])
ax[2].quiver(
X[0::ss, 0::ss], Y[0::ss, 0::ss],
Vx[0::ss, 0::ss], Vy[0::ss, 0::ss], color='b'
)
ax[2].text(
0.02, 0.02, '(c)', fontsize=24,
verticalalignment='bottom', horizontalalignment='left'
)
ax[2].set_xlabel('$x$', fontsize=24)
ax[2].set_xticklabels((0.0, 0.2, 0.4, 0.6, 0.8, 1.0), fontsize=20)
ax[2].tick_params(axis='both', which='major', labelsize=13)
fig.supxlabel("Figure 14.4", fontsize=20)
plt.show()
Finite difference discretisation¶
class PAR:
def __init__(
self, m=2, n=3, phi0=0.01, delta=1,
a_psi=1.0, a_u=1.0, a_p=1.0,
a_phi=0.1, ni=(7, 12, 22, 42, 82)
):
# physics parameters
self.n = n
self.phi0 = phi0
self.delta = delta
# manufactured solution parameters
self.m = m
self.A_psi = a_psi
self.A_U = a_u
self.A_P = a_p
self.A_phi = a_phi
self.ni = ni
def MnfcSoln_F(X, Y, par):
return - MnfcSoln_DelsqU(X, Y, par) + \
MnfcSoln_DivKGradP(X, Y, par)
def MnfcSoln_DivKGradP(X, Y, par):
phi = MnfcSoln_phi(X, Y, par)
K = np.power(phi/par.phi0, par.n)
Kx = par.n / np.power(par.phi0, par.n) * (
np.power(phi, par.n-1)
) * MnfcSoln_GradPhi(X, Y, 1, par)
Ky = par.n / np.power(par.phi0, par.n) * (
np.power(phi, par.n-1)
) * MnfcSoln_GradPhi(X, Y, 2, par)
return Kx * MnfcSoln_GradP(X, Y, 1, par) + \
Ky * (MnfcSoln_GradP(X, Y, 2, par) + 1) + \
K * MnfcSoln_DelsqP(X, Y, par)
def MnfcSoln_DelsqP(X, Y, par):
return -2.0 * np.pi**2 * par.m**2 * MnfcSoln_P(X, Y, par)
def MnfcSoln_GradPhi(X, Y, dir, par):
if dir == 1:
return -par.phi0 * np.pi * par.m * par.A_phi * \
np.sin(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
else:
return -par.phi0 * np.pi * par.m * par.A_phi * \
np.cos(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
def MnfcSoln_DelsqU(X, Y, par):
return -2.0 * np.pi**2 * par.m**2 * MnfcSoln_U(X, Y, par)
def MnfcSoln_G(X, Y, dir, par):
coeff = MnfcSoln_phi(X, Y, par) if dir == 2 else 0.0
return - MnfcSoln_GradP(X, Y, dir, par) \
+ par.delta**2 * MnfcSoln_CurlDelsqPsi(X, Y, dir, par) \
+ 3.0 * par.delta**2 * MnfcSoln_GradDelsqU(X, Y, dir, par) \
- coeff
def MnfcSoln_CurlDelsqPsi(X, Y, dir, par):
if dir == 1:
return par.A_psi * np.pi**3 * par.m**3 * (
np.cos(np.pi * par.m * X) * np.sin(np.pi * par.m * Y) - (
1.0 - np.cos(np.pi * par.m * X)
) * np.sin(np.pi * par.m * Y)
)
else:
return -par.A_psi * np.pi**3 * par.m**3 * (
np.cos(np.pi * par.m * Y) * np.sin(np.pi * par.m * X) - (
1.0 - np.cos(np.pi * par.m * Y)
) * np.sin(np.pi * par.m * X)
)
def MnfcSoln_phi(X, Y, par):
return par.phi0 * (
1.0
+ par.A_phi * np.cos(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
)
def MnfcSoln_V(X, Y, dir, par):
return MnfcSoln_CurlPsi(X, Y, dir, par) + MnfcSoln_GradU(X, Y, dir, par)
def MnfcSoln_U(X, Y, par):
return par.A_U * np.sin(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
def MnfcSoln_P(X, Y, par):
return par.A_P * np.sin(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
def MnfcSoln_GradP(X, Y, dir, par):
if dir == 1:
return par.A_P * np.pi * par.m * \
np.cos(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
else:
return par.A_P * np.pi * par.m * \
np.sin(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
def MnfcSoln_CurlPsi(X, Y, dir, par):
if dir == 1:
return par.A_psi * (
1.0 - np.cos(np.pi * par.m * X)
) * (
np.pi * par.m * np.sin(np.pi * par.m * Y)
)
else:
return -par.A_psi * (
np.pi * par.m * np.sin(np.pi * par.m * X)
) * (
1.0 - np.cos(np.pi * par.m * Y)
)
def MnfcSoln_GradDelsqU(X, Y, dir, par):
return -2 * np.pi**2 * par.m**2 * MnfcSoln_GradU(X, Y, dir, par)
def MnfcSoln_GradU(X, Y, dir, par):
if dir == 1:
return par.A_U * np.pi * par.m * \
np.cos(np.pi * par.m * X) * np.sin(np.pi * par.m * Y)
else:
return par.A_U * np.pi * par.m * \
np.sin(np.pi * par.m * X) * np.cos(np.pi * par.m * Y)
def AssembleMatrixAndRHS(phi, dx, par):
Nj, Ni = phi.shape
N = Ni*Nj
n = lambda i, j: i + j*Ni
# node position
X, Y = np.meshgrid(
dx * (np.arange(0, ni)-1),
dx * (np.arange(0, ni)-1)
)
e = np.ones(N)
# stokes equation, x - direction
APx_stk = (-1. * sp.eye(N, k=-1) + sp.eye(N, k=0))/dx # dP / dx
# delsq(u)
Axu_stk = (
sp.eye(N, k=-Ni) + sp.eye(N, k=-1) - 4.0*sp.eye(N, k=0)
+ sp.eye(N, k=1) + sp.eye(N, k=Ni)
) * (par.delta/dx)**2 + (
sp.eye(N, k=-1) - 2.0 * sp.eye(N, k=0) + sp.eye(N, k=1)
) * 2.0 * (par.delta/dx)**2 # cmp stress
# cmp stress
Acxv_stk = (
sp.eye(N, k=-1) - sp.eye(N, k=0)
+ sp.eye(N, k=Ni) - sp.eye(N, k=Ni-1)
) * 2.0 * (par.delta/dx)**2
# stokes equation, y - direction
APy_stk = (-1. * sp.eye(N, k=-Ni) + sp.eye(N, k=0)) / dx # dP / dy
# delsq(v)
Ayv_stk = (
sp.eye(N, k=-Ni) + sp.eye(N, k=-1) - 4.0 * sp.eye(N, k=0)
+ sp.eye(N, k=1) + sp.eye(N, k=Ni)
) * (par.delta / dx) ** 2 + (
sp.eye(N, k=-Ni) - 2.0 * sp.eye(N, k=0) + sp.eye(N, k=Ni)
) * 2.0 * (par.delta / dx) ** 2 # cmp stress
# cmp stress
Acyu_stk = (
sp.eye(N, k=-Ni) - sp.eye(N, k=-Ni+1)
- sp.eye(N, k=0) + sp.eye(N, k=1)
) * 2.0 * (par.delta / dx) ** 2
# compaction equation,
Au_cmp = (-1. * sp.eye(N, k=0) + sp.eye(N, k=1))/dx # div(vs)
Av_cmp = (-1. * sp.eye(N, k=0) + sp.eye(N, k=Ni))/dx # div(vs)
Kx = np.power((phi[:, 0:-1] + phi[:, 1:]) / 2.0 / par.phi0, par.n)
Ky = np.power((phi[0:-1, :] + phi[1:, :]) / 2.0 / par.phi0, par.n)
row_ind = np.zeros(((Ni-2)*(Nj-2), 5), dtype=np.int64)
col_ind = np.zeros(((Ni-2)*(Nj-2), 5), dtype=np.int64)
data_cmp = np.zeros(((Ni-2)*(Nj-2), 5), dtype=np.float64)
k = 0 # indices counter
for j in np.arange(1, Nj-1):
for i in np.arange(1, Ni-1):
# div K gradP
row_ind[k, :] = n(i, j)
col_ind[k, :] = np.asarray(
[
n(i, j-1), n(i-1, j),
n(i, j), n(i+1, j), n(i, j+1)
]
)
data_cmp[k, :] = np.asarray(
[
Ky[j-1, i], Kx[j, i-1],
-(Kx[j, i] + Kx[j, i-1] + Ky[j, i] + Ky[j-1, i]),
Kx[j, i], Ky[j, i]
]
) / (dx ** 2)
k += 1
# for div darcy flow
AP_cmp = sp.csr_matrix(
(
data_cmp.flatten(),
(
row_ind.flatten(),
col_ind.flatten()
)
),
shape=(N, N)
)
A = sp.vstack(
[
sp.hstack([Axu_stk, Acxv_stk, -APx_stk]),
sp.hstack([Acyu_stk, Ayv_stk, -APy_stk]),
sp.hstack([-Au_cmp, -Av_cmp, AP_cmp])
]
)
# right - hand side
Gx = MnfcSoln_G(X, Y + 0.5*dx, 1, par).flatten()
Gy = MnfcSoln_G(X + 0.5*dx, Y, 2, par).flatten()
F = MnfcSoln_F(X + 0.5*dx, Y + 0.5*dx, par).flatten()
b = np.hstack((Gx, Gy, F))
for j in np.arange(1, Nj - 1):
for i in np.arange(1, Ni - 1):
row = n(i, j)
# move natural forcing to the RHS, with the manufactured forcing
b[row + N] = b[row + N] + 0.5 * (phi[j, i] + phi[j-1, i])
b[row + 2*N] = b[row + 2*N] - (Ky[j, i] - Ky[j-1, i]) / dx
return A.tocsr(), b
def InsertBoundaryConditions(A, b, par, Ni, Nj, dx):
# node position
X, Y = np.meshgrid(
dx * (np.arange(0, Ni)-1),
dx * (np.arange(0, Ni)-1)
)
N = Ni*Nj
n = lambda i, j: i + j*Ni
Xl = X.flatten()
Yl = Y.flatten()
# zero u boundary rows
rows = np.hstack(
[
n(0, np.arange(0, Nj)),
n(1, np.arange(1, Nj-1)),
n(Ni-1, np.arange(0, Nj)),
n(np.arange(1, Ni-1), 0),
n(np.arange(1, Ni-1), Nj-1)
]
)
A[rows, :] = 0.0
# u boundary conditions
rows = np.hstack(
[
n(0, np.arange(0, Nj)),
n(1, np.arange(1, Nj-1)),
n(Ni-1, np.arange(0, Nj))
]
)
A[rows, rows] = 1.0
b[rows] = MnfcSoln_V(
Xl[rows], Yl[rows] + 0.5 * dx, 1, par
)
rows = n(np.arange(1, Ni-1), 0)
A[rows, rows] = 0.5
A[rows, rows + Ni] = 0.5
b[rows] = MnfcSoln_V(
Xl[rows], Yl[rows]+dx, 1, par
)
rows = n(np.arange(1, Ni-1), Nj-1)
A[rows, rows] = 0.5
A[rows, rows - Ni] = 0.5
b[rows] = MnfcSoln_V(Xl[rows], Yl[rows], 1, par)
# zero w boundary rows
rows = N + np.hstack(
[
n(np.arange(0, Ni), 0),
n(np.arange(1, Ni-1), 1),
n(np.arange(0, Ni), Nj-1),
n(0, np.arange(1, Nj-1)),
n(Ni-1, np.arange(1, Nj-1))
]
)
A[rows, :] = 0
# w boundary conditions
rows = N + np.hstack(
[
n(np.arange(0, Ni), 0),
n(np.arange(1, Ni-1), 1),
n(np.arange(0, Ni), Nj-1)
]
)
A[rows, rows] = 1.0
b[rows] = MnfcSoln_V(Xl[rows - N] + 0.5 * dx, Yl[rows - N], 2, par)
rows = N + n(0, np.arange(1, Nj-1))
A[rows, rows] = 0.5
A[rows, rows + 1] = 0.5
b[rows] = MnfcSoln_V(Xl[rows-N] + dx, Yl[rows-N], 2, par)
rows = N + n(Ni-1, np.arange(1, Nj-1))
A[rows, rows] = 0.5
A[rows, rows - 1] = 0.5
b[rows] = MnfcSoln_V(Xl[rows-N], Yl[rows-N], 2, par)
# zero P boundary rows
rows = 2*N + np.hstack(
[
n(0, np.arange(0, Nj)),
n(Ni-1, np.arange(0, Nj)),
n(np.arange(1, Ni-1), 0),
n(np.arange(1, Ni-1), Nj-1)
]
)
A[rows, :] = 0.0
# p boundary conditions
rows = 2*N + n(0, np.arange(0, Nj))
A[rows, rows] = 0.5
A[rows, rows + 1] = 0.5
b[rows] = MnfcSoln_P(
Xl[rows-2*N] + dx, Yl[rows-2*N] + 0.5*dx, par
)
rows = 2*N + n(Ni-1, np.arange(0, Nj))
A[rows, rows] = 0.5
A[rows, rows - 1] = 0.5
b[rows] = MnfcSoln_P(
Xl[rows-2*N], Yl[rows-2*N] + 0.5*dx, par
)
rows = 2*N + n(np.arange(1, Ni-1), 0)
A[rows, rows] = 0.5
A[rows, rows + Ni] = 0.5
b[rows] = MnfcSoln_P(
Xl[rows-2*N] + 0.5*dx, Yl[rows-2*N] + dx, par
)
rows = 2*N + n(np.arange(1, Ni-1), Nj-1)
A[rows, rows] = 0.5
A[rows, rows - Ni] = 0.5
b[rows] = MnfcSoln_P(
Xl[rows-2*N] + 0.5*dx, Yl[rows-2*N], par
)
return A, b
def SolveEquationsFiniteDifference(phi, dx, par):
Nj, Ni = phi.shape
N = Ni * Nj
# set up and solve discrete problem
A, b = AssembleMatrixAndRHS(phi, dx, par)
A, b = InsertBoundaryConditions(A, b, par, Ni, Nj, dx)
x = spla.dsolve.spsolve(A, b)
# reshape solution vector into fields
Vx = x[0:N].reshape(Nj, Ni)
Vy = x[N:2*N].reshape(Nj, Ni)
P = x[2*N:].reshape(Nj, Ni)
return P, Vx, Vy
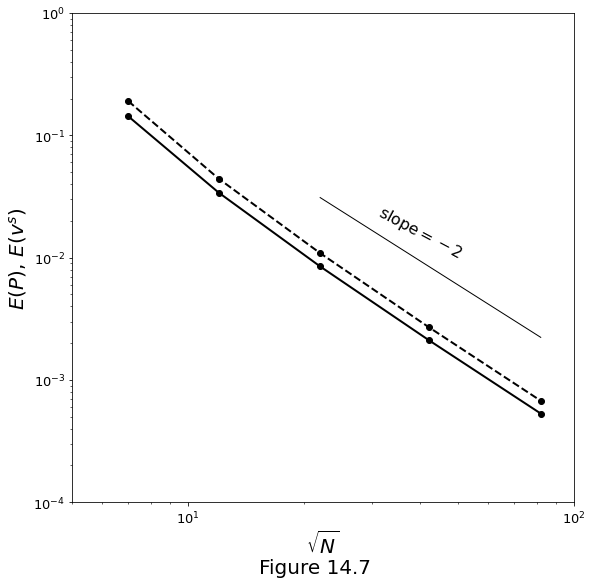
Figure 14.7 below plots the error \(\error\) versus number of nodes \(\sqrt{N}\) along one direction. Solutions are obtained by finite-difference discretisation of the Stokes/Darcy system \(\eqref{eq:num_mfcsol_gov_compaction}\)-\(\eqref{eq:num_mfcsol_gov_stokes}\). The solid line marks the velocity error; the dashed line marks the pressure error.
par = PAR()
ev, ep = [], []
for ni, nj in zip(par.ni, par.ni):
dx = 1. / (ni - 2)
# node position
X, Y = np.meshgrid(
dx * (np.arange(0, ni)-1),
dx * (np.arange(0, ni)-1)
)
# solve the finite difference problem
phi = MnfcSoln_phi(X + dx / 2, Y + dx / 2, par)
P, Vx, Vy = SolveEquationsFiniteDifference(phi, dx, par)
# exclude buffer points
P = P[1:-1, 1:-1]
Vx = Vx[1:-1, 1:]
Vy = Vy[1:, 1:-1]
V = np.hstack((Vx.flatten(), Vy.flatten()))
# manufactured solution
P_mfc = MnfcSoln_P(
X[1:-1, 1:-1]+dx/2, Y[1:-1, 1:-1]+dx/2, par
)
Vx_mfc = MnfcSoln_V(
X[1:-1, 1:], Y[1:-1, 1:]+dx/2, 1, par
)
Vy_mfc = MnfcSoln_V(
X[1:, 1:-1]+dx/2, Y[1:, 1:-1], 2, par
)
V_mfc = np.hstack(
(
Vx_mfc.flatten(),
Vy_mfc.flatten()
)
)
# compute error norms
ep.append(
np.linalg.norm(P_mfc - P) / np.linalg.norm(P_mfc)
)
ev.append(
np.linalg.norm(V_mfc - V) / np.linalg.norm(V_mfc)
)
# plotting
f, ax = plt.subplots()
f.set_size_inches(9., 9.)
ax.loglog(
par.ni, ev, '-ok', linewidth=2, label='velocity'
)
ax.loglog(
par.ni, ep,'--ok', linewidth=2, label='pressure'
)
ax.loglog(
par.ni[2:], 15./np.power(par.ni[2:], 2), '-k', linewidth=1
)
ax.set_xlabel(r'$\sqrt{N}$', fontsize=20)
ax.set_ylabel(r'$E(P),\,E(v^s)$', fontsize=20)
ax.text(
40.0, 0.01, 'slope$=-2$', fontsize=16,
rotation=-28, horizontalalignment='center'
)
ax.set_xlim(5.0, 100.0)
ax.set_ylim(1.e-4, 1.0)
ax.tick_params(axis='both', which='major', labelsize=13)
f.supxlabel("Figure 14.7", fontsize=20)
plt.show()
